| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 카카오인턴십
- 독일어독학
- 독일어
- SWIFT
- istringstream
- 카카오인턴
- 카카오코테
- c++
- 구현
- 세브란스
- 부주상골
- 독학
- DFS
- 백준
- 프로그래머스
- 코딩테스트
- SQLD
- 롯데정보통신
- sql
- dp
- 스택
- 리눅스
- 부주상골수술
- IOS
- 코테
- 부주상골수술후기
- 부주상골증후군
- ChatGPT
- BFS
- 분할정복
- Today
- Total
슈뢰딩거의 고등어
[백준] 1074 Z 분할정복 본문
https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net

분할 정복 문제이다.
각 블록에 번호를 매기는 식으로 단순 구현을 하려고 했지만, 시간 초과가 걸려서 분할정복 방법을 사용했다.
분할정복은 큰 문제를 쪼개 계산하는 방법을 말한다.
DP (동적프로그래밍) 과 비교가 자주되고, 둘의 차이는 DP 는 식의 결과를 저장해놓고 반복해서 사용하는 방식으로 각 식은 한번씩만 계산이 된다.
하지만 분할 정복은 매번 식의 결과가 동일할 것이라는 보장이 없기 때문에 식의 결과를 저장해놓고 사용하지 않는다.
먼저 이 문제는 길이가 2^n 인 정사각형으로 점점 쪼개가면서 구현을 하면 된다.
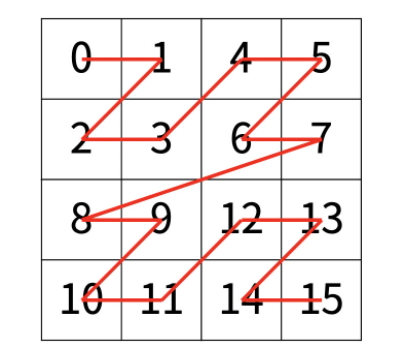
우선, 2^n의 가장 큰 정사각형을 기준으로 시작하여
그 내부에 우리가 구하고자 하는 위치가 존재한다면, 그 정사각형을 4등분한다.
만약 존재하지 않는다면, 그 블록은 분할할 필요가 없으므로 그 블록의 넓이를 리턴할 값(블록번호)에+ 해준다.
예를 들어, 우리가 찾으려는 위치가 3, 1 이라고 해보자
먼저 첫 가장 큰 정사각형 내에 존재하기 떄문에 블록을 4등분 해준다.
| 0 | 1 |
| 2 | 3 |
이 블록에는 우리가 찾으려는 위치가 존재하지 않는다. 따라서 이 블록의 넓이인 4를 블록번호에 +해준다.
| 4 | 5 |
| 6 | 7 |
마찬가지로 이 블록의 넓이인 4를 블록번호에 +해준다.
| 8 | 9 |
| 10 | 11 |
우리가 찾으려는 위치가 존재한다. 따라서 이 블록을 또 4 등분해준다.
| 8 |
| 9 |
| 10 |
각 이 블록에는 우리가 찾으려는 위치가 존재하지 않는다. 따라서 각 블록의 크기인 +1 을 블록번호에 + 해준다. (총 +3)
| 11 |
이 위치가 우리가 원하는 위치이므로 지금까지 쌓아왔던 블록번호를 return 해주고 탐색을 끝낸다.
아래 이 블록은 우리는 이미 원하는 결과를 찾았기 때문에 탐색을 할 필요가 없다.
| 12 | 13 |
| 14 | 15 |
#include <iostream>
#include <cmath>
using namespace std;
int n;
int r, c;
int no;
// y, x 탐색 시작 위치
// l 한 변의 길이
void divide_conquer(int y, int x, int l) {
if(y == r && x == c) {
printf("%d\n", no);
exit(0);
}
// 영역 안에 존재하면 분할
if(r < y+l && c < x+l) {
divide_conquer(y, x, l/2);
divide_conquer(y, x+l/2, l/2);
divide_conquer(y+l/2, x, l/2);
divide_conquer(y+l/2, x+l/2, l/2);
}
else
no += l*l;
}
int main() {
scanf("%d", &n);
scanf("%d %d", &r, &c);
divide_conquer(0, 0, pow(2, n));
}'알고리즘' 카테고리의 다른 글
| [백준] 16917 양념 반 후라이드 반 (0) | 2022.01.19 |
|---|---|
| [백준] 16968 차량번호판 (c++) (0) | 2022.01.19 |
| [백준] 1978 소수 찾기 (0) | 2022.01.18 |
| [백준] 20061 모노미노도미노2 (0) | 2022.01.17 |
| [백준] 23288 주사위 굴리기 (0) | 2022.01.17 |



